Mixture model for cluster segmentation
To help alleviate the problem of segmenting clusters of near-identical objects, we developed the TREM algorithm. This is a probabilistic template matching algorithm that fits a Gaussian-shaped, not necessarily circular, object to best fit the localization of objects in the cluster. This is done using an adapted version of the Expectation Maximization (EM) algorithm for Gaussian Mixture Models (GMM).
Experimental Collaborators
- Pohnert group at the Institute for Inorganic and Analytical Chemistry, Friedrich-Schiller University, Jena, Germany
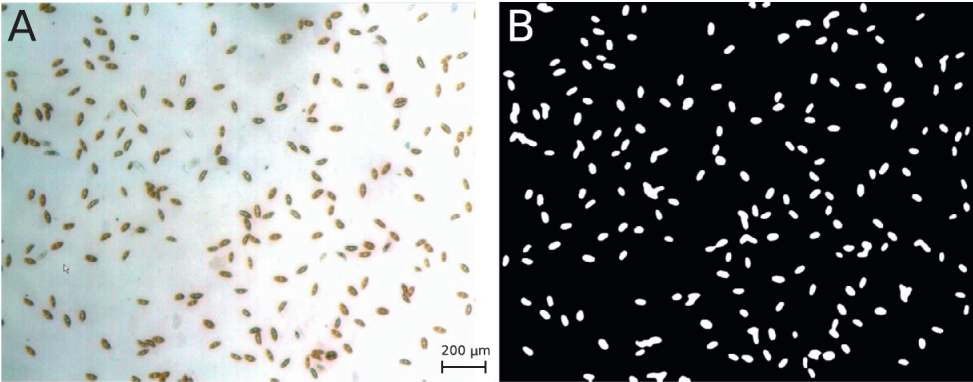
Seminavis robusta segmentation
As an example system, we use microscopy images of the marine, benthic diatom species Seminavis robusta. In (A) we see the original data and in (B) we have segmented the diatoms from the background. The segmentation was performed using standard image analysis methods, but the issue of identifying individual diatoms is not solved as we see a number of clustered diatoms in the binary image.
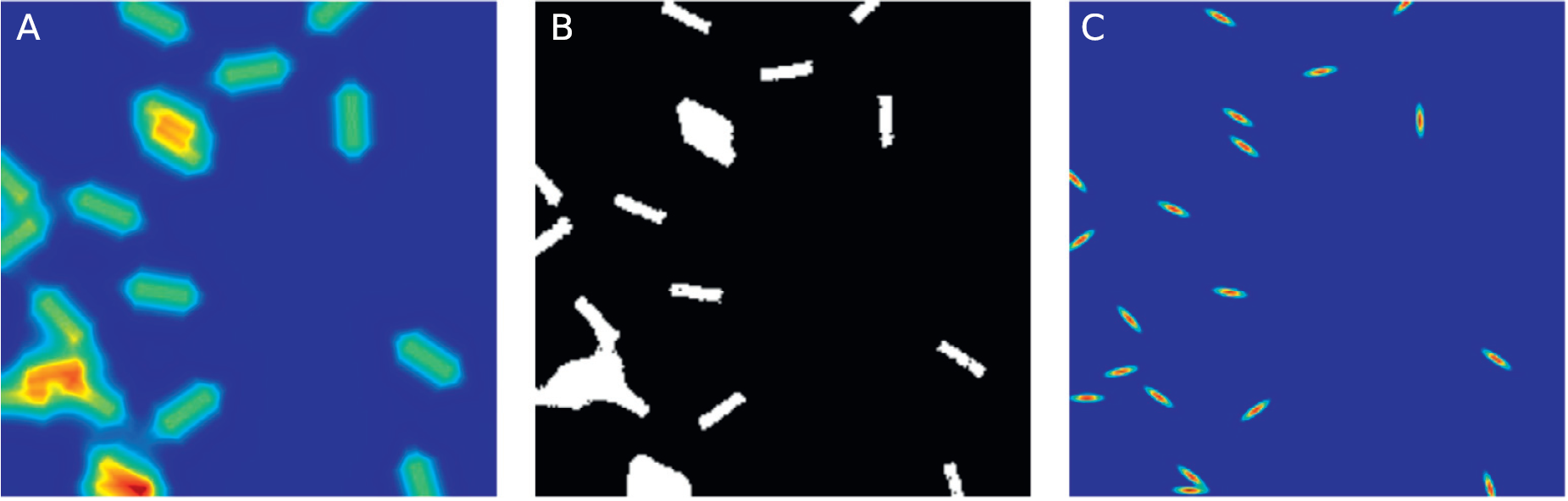
GMM representation of the data
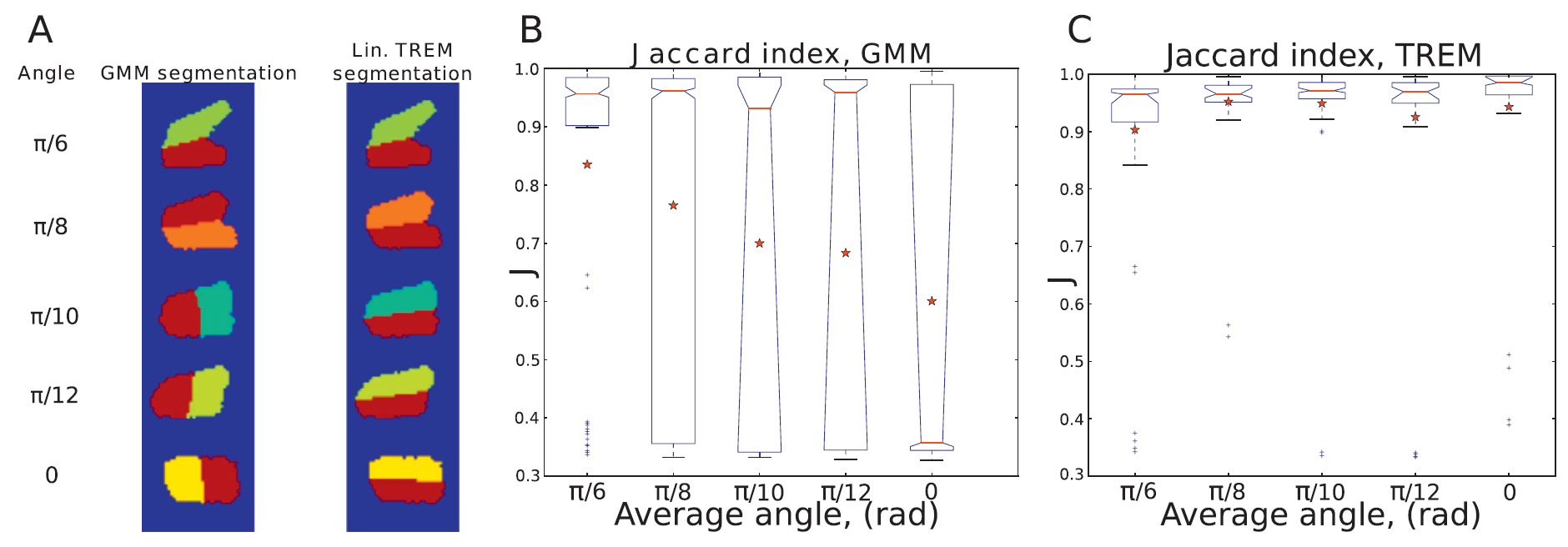
Comparison with classical GMM
The greatest advantage of TREM compared with, for example, classical GMMs without any restrictions on ΣΣ is that it is able to correctly segment near parallel objects. To demonstrate this, we generated pairs of objects with different angles between them. For each angle, we generated 30 pairs and subjected the positions and exact angles to some noise. In (A) we show example pairs of these objects with colors indicating the resulting segmentation of TREM and unconstrained GMM. For the average angle π/6π/6 we see that the segmentation, as measured by the Jaccard index in (B) and (C), is successful in almost all cases for both methods, but as the angle decreases, the GMM starts splitting the clusters along the wrong axis. TREM is consistently performing the correct segmentation with very few mistakes.
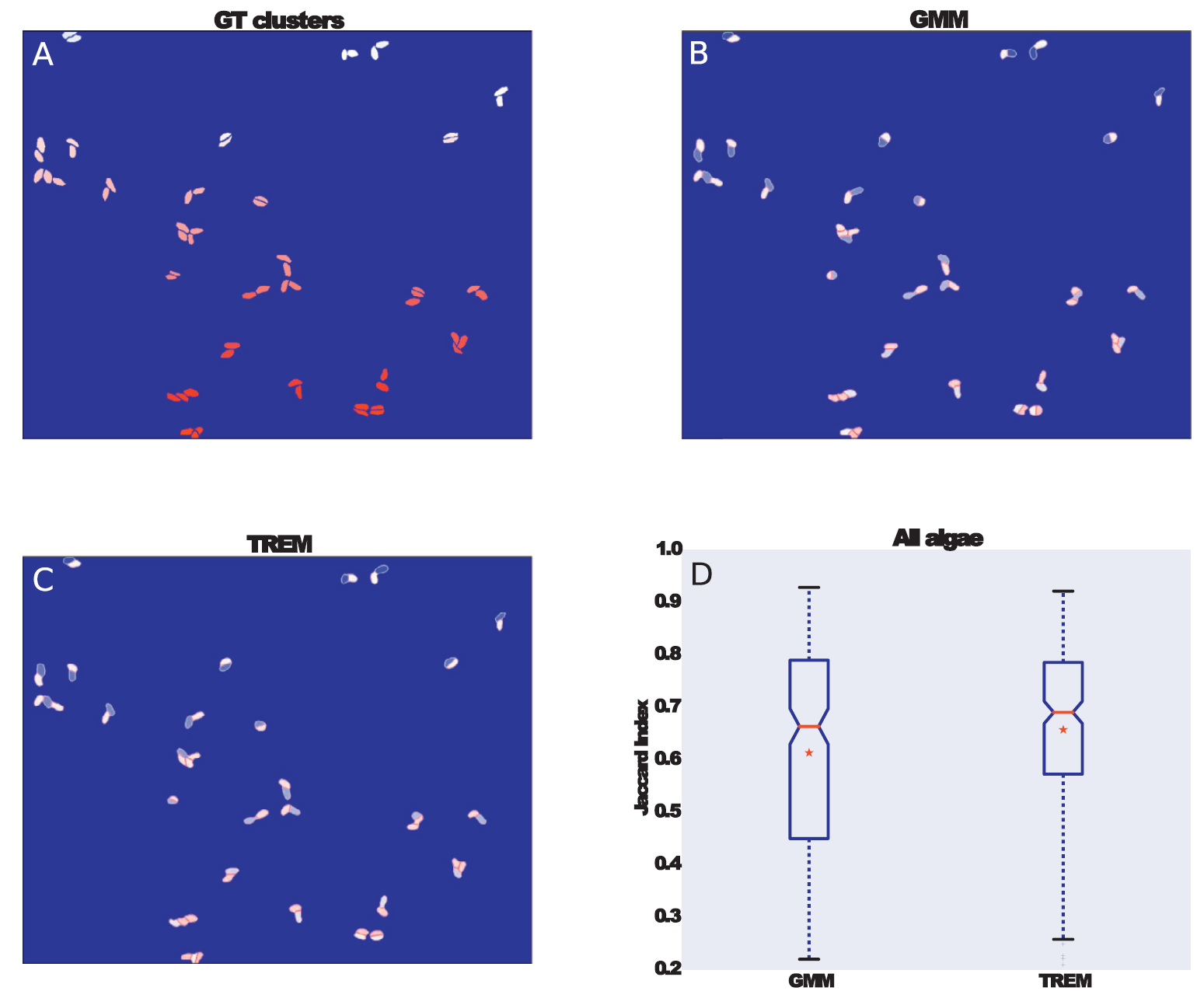
Application to diatom data
The final test is to apply TREM to the real data, in this case, the marine, benthic diatom species Seminavis robusta. In (A) we see some of the manually segmented diatoms, while in (B) and (C) we see the segmentation results from unconstrained GMM and TREM respectively. In (D) we summarize the results by plotting the Jaccard index of the segmentation by the two algorithms for 248 diatom clusters in the data. We can see that TREM performs better by having fewer really low results and in the bottom right of (B) and (C) we can see how TREM successfully segment near parallel objects while the GMM fails on those.